¿Cuál es la diferencia entre el interés simple y el compuesto? ¿Cómo se calculan? Para una mejora radical de tus finanzas, es fundamental que conozcas ambos conceptos porque te darás cuenta de que actúan de forma exponencial. Algunos lo llaman la "magia del interés compuesto", nosotros preferimos explicarte que son matemáticas puras y que ponerlo en práctica está al alcance de todos.
|
Diferencia entre interés simple e interés compuesto Calculadora interés simple y compuesto Calculadora de interés compuesto con aportaciones periódicas |
Diferencia entre interés simple e interés compuesto
Básicamente la diferencia está en que en el interés simple, el dinero que generan los intereses se calcula solo sobre el capital invertido al principio (principal) sin tener en cuenta la posible reinversión de los intereses que vaya generando nuestro dinero. Por otro lado, en el interés compuesto los intereses obtenidos se reinvierten creando con el paso del tiempo un "efecto bola de nieve" y obteniéndose un resultado sensiblemente mayor.
Calculadora del interés simple y compuesto
En el siguiente simulador, puedes calcular los intereses que obtendrías con interés simple y con interés compuesto, teniendo en cuenta el mismo capital inicial (cantidad), tipo de interés y periodo de tiempo. Ten en cuenta que en el resultado estaría incluido el capital inicial, es decir, sería la suma final de los intereses más la cantidad inicial.
Calculadora de interés
Cantidad: euros
Tipo de interés: %
Tiempo: años
Interés simple:
Interés compuesto:
Calculadora del interés compuesto con aportaciones periódicas
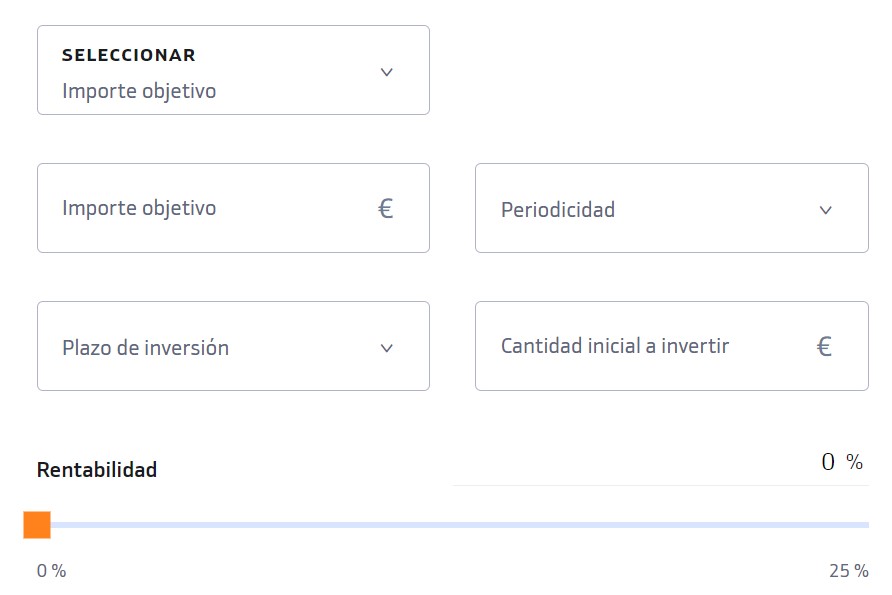
En Bankinter hemos desarrollado una herramienta que te ayudará a calcular cuánto dinero puedes ahorrar en función de tu plazo de inversión, de las cuotas mensuales y de la periodicidad de las mismas. Acceder a la calculadora.
Ejemplo sobre el interés simple y el interés compuesto
Imaginemos que tenemos 10.000 euros ahorrados y los invertimos conseguiendo un 10% de interés anual durante 30 años.
En el caso del interés simple, recibiríamos 1.000 euros de intereses el primer año, el segundo año, el tercer año... y así sucesivamente. Cada año, retiraríamos esos 1.000 euros y simplemente seguiríamos consiguiendo el 10% de 10.000 euros cada 12 meses. Esto sería así porque el capital sobre los que se calculan los intereses se mantendría invariable en los 10.000 euros iniciales.
En el caso del interés compuesto, los 1.000 euros que consigo de intereses los reinvertiría y permitiría que el 10% fuese "trabajando" cada cada vez sobre una cantidad mayor. El primer año, obtendría 1.000 euros, los sumaría a los 10.000 iniciales y pondría a "trabajar" 11.000 euros el segundo año. Esos 11.000 euros al 10% de interés, generarían ya al año siguiente 1.100 euros de intereses. Los reinvierto y tendría una nueva cantidad de 12.100 euros sobre los que calcular la rentabilidad. Generaría 1.210 euros. Y así sucesivamente durante 30 años.
En los primeros años, las diferencias existen pero no son muy abultadas. Sin embargo, tal y como se observa en el gráfico a medida que pasa el tiempo esas diferencias son cada vez más y más grandes, hasta tal punto que en el último año estaré generando un interés anual de 15.863 euros en el caso del interés compuesto y solo 1.000 euros en el caso del interés simple.
Si sumamos las cantidades obtenidas en ambos casos, vemos como en el caso del interés simple acabaré con 40.000 euros (10.000 iniciales y 30 pagos de 1.000 euros cada año) y que en el caso del interés compuesto terminaré con un montante acumulado de 174.494 euros (10.000 euros de inicio y 134.494 euros de intereses). La diferencia es muy llamativa como puede verse en la siguiente tabla y gráfico correspondiente.
|
Año |
Interes simple |
Interés compuesto |
| 0 | 10.000 (inicial) | 10.000 (inicial) |
| 1 | 11.000 | 11.000 |
| 2 | 12.000 | 12.100 |
| 3 | 13.000 | 13.310 |
| 4 | 14.000 | 14.641 |
| 5 | 15.000 | 16.105 |
| 6 | 16.000 | 17.716 |
| 7 | 17.000 | 19.487 |
| 8 | 18.000 | 21.436 |
| 9 | 19.000 | 23.579 |
| 10 | 20.000 | 25.937 |
| 11 | 21.000 | 28.531 |
| 12 | 22.000 | 31.384 |
| 13 | 23.000 | 34.523 |
| 14 | 24.000 | 37.975 |
| 15 | 25.000 | 41.772 |
| 16 | 26.000 | 45.950 |
| 17 | 27.000 | 50.545 |
| 18 | 28.000 | 55.599 |
| 19 | 29.000 | 61.159 |
| 20 | 30.000 | 67.275 |
| 21 | 31.000 | 74.002 |
| 22 | 32.000 | 81.403 |
| 23 | 33.000 | 89.543 |
| 24 | 34.000 | 98.497 |
| 25 | 35.000 | 108.347 |
| 26 | 36.000 | 119.182 |
| 27 | 37.000 | 131.100 |
| 28 | 38.000 | 144.210 |
| 29 | 39.000 | 158.631 |
| 30 | 40.000 | 174.494 |
Fórmula del interés simple
La fórmula del interés simple es más sencilla que la del interés compuesto, como podríamos imaginar. Se calcula multiplicando el Capital o principal por la tasa de interés y el tiempo:
I (interés) = C (capital) * R (tasa de interés) * T (tiempo)
Si en lugar de hablar de años, fuera en meses, simplemente dividiríamos el tiempo entre 12, de este modo:
I = C * R * T (meses) / 12
Por último también podría hablarse de días, en ese caso se utilizaría como base del año 360 días (12 meses de 30 días).
I = C * R * T (días) / 360
Como veis es un método muy sencillo. La desventaja de este método es que no tiene en cuenta los intereses acumulados de un periodo a otro, por lo cuál en el mundo de las finanzas muchas veces no resulta práctico. Por ejemplo en el caso de la cuenta COINC, en el que se va acumulando el dinero que obtenemos, debemos utilizar el interés compuesto para saber cuánto vamos a tener en una fecha determinada.
Fórmula del interés compuesto
Para calcular el capital final lo que haremos es multiplicar el capital inicial por uno más los intereses, elevado al número de periodos. Como veis en la fórmula hemos añadido una "n", esto representaría el número de veces que el interés se capitaliza al año. Por ejemplo, como COINC lo hace mensualmente, ese número sería 12.
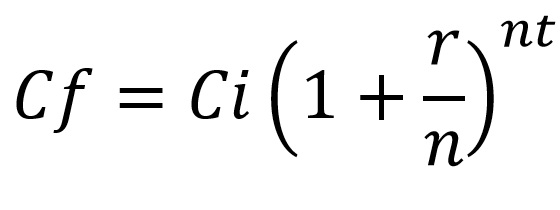
Debemos tener en cuenta que podemos encontrar muchas fórmulas parecidas, en las que se dice básicamente lo mismo pero se muestra con otras letras. Estas serían las equivalencias:
- Capital final Cf = Valor final (VF)
- Capital inicial Ci = Valor actual (VA)
- La tasa de interés puede representarse con una r o con una i.
- El tiempo puede representarse con una t o con una n
Entender el funcionamiento del interés simple y compuesto y ponerlo en práctica es fundamental si se quiere gonzar de una buena salud financiera. Son muchas las personas que se sorprenden al conocerlo y muchas las que, tras hacerlo, se arrepienten de no haber empezado antes a ahorrar e invertir porque se dan cuenta que cuantos más años la pongan en funcionamiento más intereses conseguirán generar.
Por eso es tan importante empezar a ahorrar e invertir cuanto antes, ya sea para nuestra jubilación o simplemente para gozar cuanto antes de una estupenda salud financiera. Ya que los años cumplidos... no vuelven.
A la hora de obtener un tipo de interés, no solo hay que pensar en depósitos sino que todo es también aplicable a inversiones, por ejemplo acciones o fondos. Lo que irá variando serán los porcentajes y los resultados, pero la filosofía es la misma. También está la opción de aportaciones periódicas u otros métodos. Publicidad